General Nerdocracy

2010-04-02

by Darknut

Poker Chips Distribution Calculator

Leave a nerd alone for a couple hours with some poker chips, and see what happens? He wants the chips given to each player to add up to a value corresponding to the buy-in (or a multiple thereof). He wants the ratio of colors to be practical. And he wants a systematic answer, perhaps defined by a series of equations.

Frustrated by a hazy memory of high school algebra, he turns to brute force C++.

A test to show that the algorithm is sound.

The colored blocks on the right show visually how many of each color go to each player. The left columns show how many chips altogether, regardless of value, go to each player; the value of all those chips; and the maximum number of players possible, given the total chips in the set.

This run is restricted to only distributions that give each player 25 to 50 chips, and that add up to $500.
This means that for a $5 buy-in, each white chip is worth exactly 1 cent.

I figured out some of these combinations by hand, but this program reveals many more that I hadn't considered (mainly because of the ungainly ratio of denominations).

Inputs:

• Number of chips available in each denomination.
• Value of each denomination.
• Color of each denomination.
• Desired number of starting chips per player (default 25 to 50).
• Desired starting value of each player's chips (optional).
• Minimum number of players (optional).

Distributions with more higher chips than lower chips are not allowed. This means that a distribution with no whites, or no reds, or fewer whites than reds, and so on is not considered.

It's hard to further define a preferred ratio of colors, partly because so far, I haven't been able to express a reason to eliminate any more of the answers, even the disproportionate-looking ones. Sometimes it's hard to put a feeling about something like proportions into terms the computer can execute.

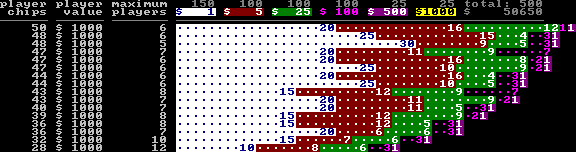Save as above, except restricted to $1000 per player.

If you don't specify a desired starting value for each player's chips, then there are like a bazillion answers. (Which is probably why it's so easy to not care that your chips represent an exact multiple of the buy-in.)

If you specify the minimum number of players, then the bazillion answers are reduced somewhat. Interesting curve below.

Restricted to only distributions that give each player 25 to 50 chips, and that support at least 15 players.

The curve has a similar repeating pattern if I change the min. players a bit. Apparently my set of chips cannot support a game with more than 18 players (3rd from the bottom) unless I break the "you must have at least as many whites as reds" rule, or unless I give each player less than 25 chips to start. I'm sure that 18 players would be "stretching it" because players in need of change would become a problem. And don't forget about re-buys. It's probably more realistic to get more chips if you were going to have a game that big.

In retrospect I don't think high school algebra provides a method for solving this many unknowns. But it's hard for me to remember.

iPhone version coming soon! (Not.)

Comment